スネルソンのテンセグリティ彫刻は確かに美しい。
しかしその最大の弱点が、
テンセグリティ概念（＝不連続の連続）とその定義のみならず
“テンセグリティ”という名称自体をもバックミンスター・フラーから借用し、
それらを自身の諸作品に複製すると同時に、
この複製芸術が「純粋な構造」に転用されることを
半世紀も拒んできた歴史にあることは、
知っておくべきだろう。
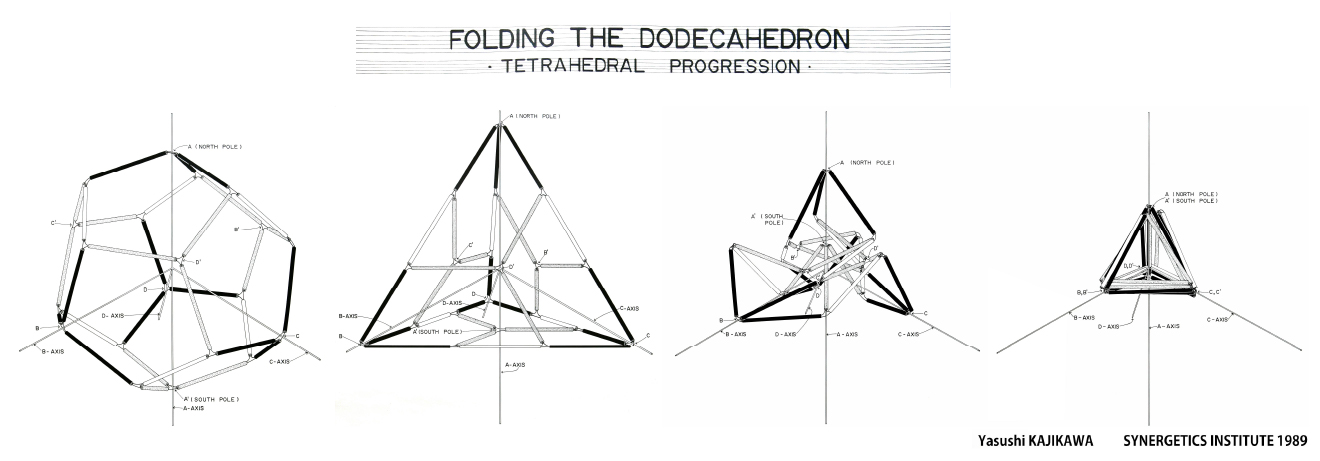
バックミンスター・フラーは純粋な「自然の構造」を
1949年に発見していた。
テンセグリティという概念が芸術作品よりも先行していた事実は、
シナジェティクスにおいて「物質の遅延」として認識される。
Kenneth Snelson: 1962 Patent Drawings (abandoned)
Kenneth Snelson:Triangle Planar Piece Model, 1961
テンセグリティの構造デザインに独創はいらない。
圧縮材と張力材が統合された
構造の安定性に自己表現は不要だ。
鳥は無駄のない翼の形態と機能を自己表現するために
飛行することはしないだろう。
構造を自律させるための膨大な試行錯誤は
自己表現の対象ではない。
新たな構造原理の発見がこそが
前例のないエンジニアリングの閃きを
もたらすにちがいない。
自然を模倣して新たな構造が発見できるなら
顕微鏡の発明と共に
テンセグリティ構造は発見されていたにちがいない。
テンセグリティ構造を
モデルに置換し純粋に構造化するには
その発明よりも前に
新たな構造原理の発見を待たなければならなかった。
そして、この21世紀においては
テンセグリティ構造を
人類の生存のために実用化するには
バックミンスター・フラーの定義にも依存しない
新たな構造原理が発見されるかもしれない。
テンセグリティ構造は
その定義と共に
自然の形態的模倣からは発見できないように
デザインされているからだ。
テンセグリティ構造は
認識にとっても革命的な存在である。
Fig. 401.00 Tensegrity Tetrahedron with “Me” Ball Suspended at Center of Volume of the Tetrahedron: Note that the six solid compression members are the acceleration vectors trying to escape from Universe at either end, by action and reaction; whereas the ends of each would-be escapee are restrained by three tensors, one long and two short; while the ball at the center is restrained from local torque and twist by three triangulated tensors tangentially affixed from each of the four corners.
by RBF
Tension as gravity: a tension structure is nature’s fundamental pattern-cohering principle.
by R.B.F
自然には
質の悪い張力材はない。
まずい重力がないように。
太陽系は重力によって
ダイナミックに統合された
テンセグリティシステムである。
しかし、惑星地球では
圧縮材を統合するためには
重力という張力材だけでは不十分だ。
物質のテンセグリティ化には
統合する意志が
張力による統合化よりも
先行している必要がある。
無論、その意志にも
「良い・悪い」はなく、
あるのは
「強い・弱い」でしかない。
テンセグリティは
ギリシア人の考えた球の概念に基づいて
同一球面に内接すると思われているが
中心からその球面までの
すべての半径が同一になる
瞬間は存在しない。
なぜなら、テンセグリティは外力を受けて
つねに振動しているからである。
本質的に振動するテンセグリティは
時間の経過によってはじめて
統計的に非固体的な球面を形成するのである。
球面は同時には存在しない。
解説 梶川泰司
Fig. 770.11 System Turbining in Tensegrity Structures:by RBF
テンセグリティは万有引力と同じように
ユニバーサルである。
その張力機能には長さの限界がない。
自然は張力を距離を超えて
ユニバーサルにデザインしている。
文化・言語・国籍・性別・年齢の違いを超えて
利用できる製品・情報の人間工学理論から
テンセグリティは生まれなかった。
断面積ゼロの
重力という張力のユニバーサル・デザインは
あまねく太陽系から学ぶことができる。
圧縮材に張力材を引っかければ、
テンセグリティになるのではなく
圧縮材で張力材を押し拡げれば
テンセグリティになるのである。
魚を捕るための網が
逃げ惑う無数の魚によって
つねに球状に非同時的に
押し広げられるように。
解説 梶川泰司
ninety-strut-geodesic-dome-tensegrity
thomas-zung-buckminster-fuller-sadao-zung.
バックミンスター・フラーの
テンセグリティモデルとその概念スケッチ
Fig. 762.01 Chordal Ricochet Pattern in Stretch Action of a Balloon Net by RBF
科学的な構造の定義が
バックミンスター・フラーによる
テンセグリティ原理の発見から導き出された以上、
新しいコンポジットから構成される
21世紀の構造は、
盗作であるか革命であるか、
そのいずれかだ。
もしそれが革命の方ならば、
もう1つのテンセグリティ原理が
そこには潜んでいることになる。
Fig. 730.12 Stabilization of Tension in Tensegrity Column by R.B.F
21世紀のエンジニアはテンセグリティーの有効性に同意する。
しかし、彼らは未だに圧縮構成要素を計算する技術だけで
テンセグリティの構造化の可能性を判断している。
引張による構造化には大きさの限度がないという
＜張力の完全性＞を除外したまま。
新たな水力学的および空気力学的エンジニアによって
テンセグリティーを開発しなければならない。
真の構造を求めると
自律的エンジニアリングを形成するのである。
テンセグリティによって
形態学（morphology)に飛躍をもたらした
シナジェティクスは
形態学からテンセグリティという
構造システムを発見したのではない。
前例のないこの構造システムをもっとも鮮やかに説明する
doing more with lessという方法は
可視的な自然の観察方法から発見できなかった。
シナジェティクスを
複数の異なったモデリングから理解すると
短時間に科学、数学と工学
そして教育制度の欠点を発見できるのは偶然ではない。
そして、お金と富の違い、
そして産業と銀行と有価証券の特徴と役割などの
経済学の基本さえも理解できるのは
人間が引き起こすdoing more with lessでない＜アブノックス現象＞を
自然の構造と比較できるからにちがいない。
シナジェティクスは
不可視の自然に対する
もっとも包括的なメタフィジックスである。
それゆえに
もっとも直観的で信頼できる非・形態学である。
Circuit Pattern Tensegrity by R.B.Filler
Fig. 1033.019
In Anthony Pugh’s model 12 struts form four interlocking but nontouching triangular circuits.
The plane of each triangle of struts bisects the vector equilibrium which its vertexes define.
Each triangle of struts is inscribed within a hexagonal circuit of tensors.